Difference between Budding And Grafting > 자유게시판

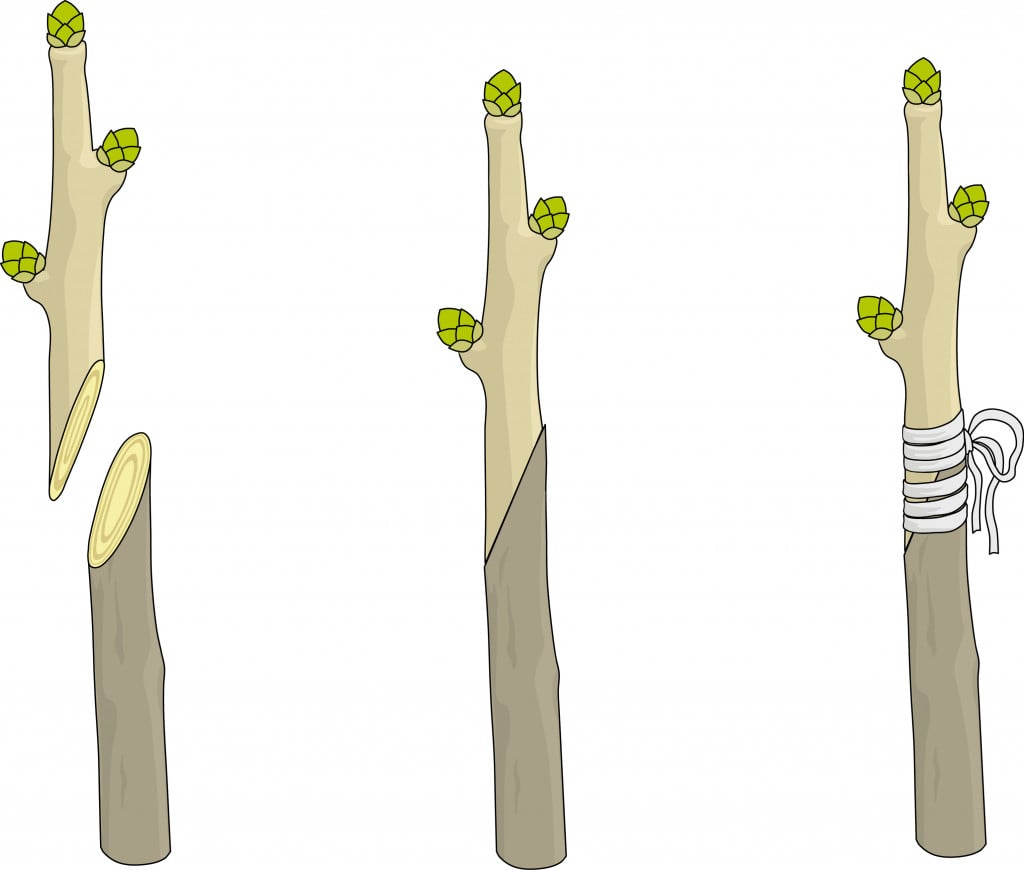
Both budding and grafting are two completely different, important processes used for the manufacturing of latest plants. One of these plant breeding refers to vegetative propagation. Vegetative propagation refers to an asexual mode of reproduction in plants, which is primarily produced by the vegetative elements of older plants, and these embody roots, stems and leaves. This type of asexual reproduction in plants has a number of benefits, each biological and genetic. Both budding and grafting strategies help in growing the productivity of certain horticultural crops. In this strategy of horticulture methods, chosen plants are of intently related species, giving rise to new disease-free and wholesome plants that are in a position to tolerate drought. Budding is a technique whereby small buds are collected from one plant and grown on one other. Examples of plants produced by budding methods embody cherry, citrus fruits, ornamental plants, peach, apple, plums and nut timber. Explore more: Budding in Hydra and Yeast. grafting (cesarvayt23355.shoutmyblog.com) is a technique practised by reducing, becoming a member of the components of two completely different plants and rooting in the ground. After some days, the tissues of the graft turn out to be built-in with the tissues of the rooted plant and develop as a single plant over time. Here, in this horticultural technique, the different elements of plants are used for producing new plants. There are a number of methods followed in the strategy of grafting, which embody - bark grafting, cleft grafting, saddle grafting, aspect veneer grafting and splice grafting.

Flood fill, also referred to as seed fill, is a flooding algorithm that determines and alters the area connected to a given node in a multi-dimensional array with some matching attribute. It is used within the "bucket" fill instrument of paint applications to fill connected, similarly-colored areas with a special color, and in video games resembling Go and Minesweeper for figuring out which pieces are cleared. A variant referred to as boundary fill uses the identical algorithms however is outlined as the area related to a given node that doesn't have a specific attribute. Note that flood filling shouldn't be suitable for drawing stuffed polygons, as it is going to miss some pixels in more acute corners. Instead, see Even-odd rule and Nonzero-rule. The standard flood-fill algorithm takes three parameters: a begin node, a goal coloration, and a alternative color. The algorithm appears for all nodes in the array which might be connected to the start node by a path of the target coloration and modifications them to the alternative colour.

For a boundary-fill, instead of the goal coloration, a border shade would be provided. So as to generalize the algorithm in the widespread manner, the next descriptions will instead have two routines available. One called Inside which returns true for unfilled factors that, by their color, can be contained in the crammed area, and one referred to as Set which fills a pixel/node. Any node that has Set known as on it must then no longer be Inside. Depending on whether we consider nodes touching on the corners related or not, we now have two variations: eight-manner and 4-approach respectively. Though straightforward to know, the implementation of the algorithm used above is impractical in languages and environments the place stack area is severely constrained (e.g. Microcontrollers). Moving the recursion into a knowledge structure (both a stack or a queue) prevents a stack overflow. Check and set every node's pixel coloration earlier than including it to the stack/queue, lowering stack/queue size.

Use a loop for the east/west directions, queuing pixels above/below as you go (making it just like the span filling algorithms, under). Interleave two or more copies of the code with extra stacks/queues, to permit out-of-order processors more alternative to parallelize. Use a number of threads (ideally with barely different visiting orders, so they do not keep in the same space). Very simple algorithm - easy to make bug-free. Uses numerous reminiscence, particularly when using a stack. Tests most stuffed pixels a total of 4 times. Not suitable for sample filling, as it requires pixel take a look at outcomes to change. Access pattern is not cache-friendly, for the queuing variant. Cannot easily optimize for multi-pixel words or bitplanes. It's potential to optimize things additional by working primarily with spans, a row with fixed y. The primary published complete instance works on the following fundamental precept. 1. Starting with a seed level, fill left and right.

Keep track of the leftmost filled level lx and rightmost stuffed point rx. This defines the span. 2. Scan from lx to rx above and beneath the seed point, searching for brand new seed points to continue with. As an optimisation, the scan algorithm doesn't need restart from each seed level, but solely those at the start of the next span. Using a stack explores spans depth first, whilst a queue explores spans breadth first. When a new scan would be totally inside a grandparent span, it will definitely only discover filled pixels, and so wouldn't want queueing. Further, when a new scan overlaps a grandparent span, solely the overhangs (U-turns and W-turns) should be scanned. 2-8x sooner than the pixel-recursive algorithm. Access pattern is cache and bitplane-friendly. Can draw a horizontal line slightly than setting particular person pixels. Still visits pixels it has already stuffed. For the favored algorithm, three scans of most pixels. Not suitable for sample filling, because it requires pixel take a look at outcomes to alter.